Vishisht Ushma Ka Sutra विशिष्ट ऊष्मा का सूत्र
विशिष्ट ऊष्मा का सूत्र
सही उत्तर : विशिष्ट ऊष्मा का विमीय सूत्र [L2T-2θ-1]
यह एक सामान्य अनुभव है कि किसी वस्तु का ताप बढ़ाने के लिये उसे उष्मा देनी पड़ती है। किन्तु अलग-अलग पदार्थों की समान मात्रा का ताप समान मात्रा से बढ़ाने के लिये अलग-अलग मात्रा में उष्मा की जरूरत होती है। किसी पदार्थ की इकाई मात्रा का ताप एक डिग्री सेल्सियस बढ़ाने के लिये आवश्यक उष्मा की मात्रा को उस पदार्थ का विशिष्ट उष्मा धारिता (Specific heat capacity) या केवल विशिष्ट उष्मा कहा जाता है। इससे स्पष्ट है कि जिस पदार्थ की विशिष्ट उष्मा अधिक होगी उसे गर्म करने के लिये अधिक उष्मा की आवश्यकता होगी। उदाहरण के लिये, शीशा (लेड) का ताप डिग्री सेल्सियस बढ़ाने के लिये जितनी उष्मा लगती है उससे आठ गुना उष्मा एक किलोग्राम मग्नीशियम का ताप डिग्री सेल्सियस बढ़ाने के लिये आवश्यक होती है। किसी भी पदार्थ की विशिष्ट उष्मा मापी जा सकती है। तापवृद्धि के समय बाह्य स्थिति के अनुसार पदार्थों की विशिष्ट उष्मा के अनेक मान होते हैं। एक तो स्थिर आयतनवाली विशिष्ट उष्मा होती है जो उसकी आंतरिक ऊर्जा से संबंधित रहती है। मापन क्रिया के समय आयतन में परिवर्तन होने के कारण आयतनवृद्धि के लिए कार्य करना पड़ता है और तापवृद्धि के साथ साथ कुछ उष्मा की इस काम के लिए भी आवश्यकता होती है। काम की मात्रा दाब के आश्रित है और यदि यह दाब स्थिर न हो तो यह मात्रा भी परिवर्तित होगी। इसीलिए स्थितियों में भेद होने के कारण विशिष्ट उष्मा के अनेक मान होते हैं, किन्तु सुविधा के लिए केवल दो पर ही विचार किया जाता है। एक का सम्बन्ध स्थिर आयतन और दूसरे का स्थिर दाब से है और इनको क्रमानुसार Cv और Cp लिखा जाता है। ठोसों और द्रवों में तापीय प्रसरण अपेक्षाकृत कम होता है, अत: विशिष्ट उष्मा के अनेक मान लगभग बराबर होते हैं किन्तु गैसों में इनमें बहुत अन्तर होता है। बहुपरमाण्वीय अणुओं में विशिष्ट उष्मा को अणुभार से गुणा करने पर उनकी आणव उष्मा (मॉलिक्युलर हीट) और एक परमाणुक अणुओं में विशिष्ट उष्मा को परमाणुभर से गुणा करने पर उनकी पारमाण्वीय उष्मा (ऐटॉमिक हीट) प्राप्त होती है। इस संबंध में आदर्श गैसों में यह सूत्र लागू होता है: यहाँ पर R पूर्ववर्णित गैस नियतांक है। सन् 1819 में डयूलांग और पेटिट ने यह नियम प्रतिपादित किया कि सब ठोस तत्वों की स्थिर आयतनवाली पारमाण्वीय उष्मा एक ही होती है और उसका मान 5.94 कलरी/ग्राम परमाणु डिग्री सेल्सियस होता है। शीघ्र ही प्रयोगों द्वारा यह सिद्ध हुआ कि हल्के तत्व कार्बन, बोरॉन और सिलिकन - इस नियम के अपवाद हैं। पूर्ववर्णित नर्न्स्ट के प्रयोगों से यह ज्ञात हुआ कि ताप कम होने पर यह नियम किसी भी ठोस पर लागू नहीं होता और ताप घटने पर सब तत्वों की पारमाण्वीय उष्मा घटती जाती है, यहाँ तक कि परम शून्य के निकट लगभग शून्य हो जाती है। किसी तन्त्र (सिस्टम) की ऊर्जा के व्यंजक में जितने वर्ग (स्क्वेयर) पद आते हैं उनकी संख्या उस समुदाय की स्वतंत्रता संख्या (डिग्रीज़ ऑव फ्रीडम) कहलाती है। एकपरमाणुक आदर्श गैसों में यह संख्या प्रति अणु और ठोस तत्वों में यह प्रति परमाणु होती है। डयूलांग और पेटिट के नियम की निम्न ताप पर विफलता को आइंस्टाइन ने 1907 में प्लांक के क्वांटम सिद्धांत के आधार पर समझाने का प्रयास किया। इस सिद्धान्त के अनुसार कोई भी n आवृत्तिवाला दोलक ऊर्जा का शोषण अथवा उत्सर्जन केवल h n बंडलों अर्थात् क्वांटमों में ही करता है। यहाँ h प्लांक स्थिरांक है। आइंस्टाइन ने सब परमाणुओं की आवृत्तियाँ एक ही मानकर पारमाण्वीय उष्मा की गणना की और प्रायोगिक परिणामों को मोटे रूप से समझाया। आइंस्टाइन ने स्वयं ही स्वीकार किया था कि उसका सब परमाणु की एक ही आवृत्ति मानना उचित नहीं था। डिबाई ने संपूर्ण ठोस को अविरत (कंटिनुअस) मानकर गणना की कि यह ठोस कुल कितने प्रकार से दोलन कर सकता है। अविरत ठोस में यह संख्या अनन्त होती है और इस कारण पारमाण्वीय उष्मा भी अनन्त ही होनी चाहिए। इससे बचने के लिए डिबाई ने यह निराधार कल्पना की कि एक विशिष्ट आवृत्ति से ऊपर किसी दोलन की सम्भावना नहीं। यह आवृत्ति ऐसी होती है कि उससे नीचेवाली समस्त आवृत्तियों की कुल संख्या 3N होती है। बहुत समय तक डिबाई का सिद्धान्त प्रायोगिक परिणामों को समझाने में सफल रहा, किन्तु कुछ समय पश्चात् उसकी यर्थाथता कम हो गई। बॉर्न ने ठोस के क्रिस्टलीय स्वरूप को ध्यान में रखा और दोलन वर्णक्रम (स्पेक्ट्रम) को ऐसी आवृत्ति पर समाप्त किया जिसके तरंगदैर्घ्य का संबंध माणिभ की बनावट से है। यह समाप्ति क्रिस्टल की बनावट पर आधारित होने के कारण डिबाई की आवृत्ति समाप्ति से श्रेष्ठ है। बॉर्न के सिद्धांत का ब्लैकमैन, कैलरमैन इत्यादि ने विकास किया और इसके द्वारा प्रायोगिक परिणामों की सफलतापूर्वक व्याख्या की। भारतीय वैज्ञानिक चन्द्रशेखर वेंकट रमण ने यह सिद्धान्त प्रतिपादित किया कि किसी भी उष्मिक दोलन को सम्पूर्ण ठोस का दोलन मानना त्रुटिपूर्ण है। उनके अनुसार कोई भी उष्मिक दोलन केवल कुछ परमाणु समुदाय का दोलन होता है और प्रत्येक दोलन का यह रूप होता है कि उनमें निकटस्थ किस्ट्रल सेलों में ऊर्जा की मात्रा बराबर होती है। विश्वेश्वरदयाल ने रमण के सिद्धांत द्वारा अनेक ठोसों की पारमाण्वीय उष्मा की गणना की और उनका प्रायोगिक फलों से मेल सिद्ध किया। सिद्धान्ततः भिन्न होने पर भी रमण और बॉर्न के सिद्धान्तों द्वारा गणना की हुई पारमाण्वीय उष्मा के मान में विशेष अन्तर नहीं पाया जाता। गैसों की आणव उष्मा की गणना करने के लिए उसको तीन भागों में विभक्त किया जाता है जिनका सम्बन्ध क्रमानुसार सरल गति, घूर्णन गति और दोलन से होता है। यदि किसी गैस अणु में n परमाणु हों तो उसकी कुल स्वतंत्रता संख्या (3n) होती है जिसमें तीन सरल गति से, दो या तीन घूर्णन से और शेष दोलन से सम्बंधित हैं। सरल गति से उत्पन्न आणव उष्मा प्रति स्वंतत्रता-संख्या 1/2k होती है। यदि अणुभार और ताप बहुत कम न हों तो यही प्रभाव घूर्णन का भी होता है, परन्तु इनके कम होने पर घूर्णन के प्रभाव की क्वाण्टम सांख्यिकी द्वारा गणना की जाती है। दोलन का प्रभाव ठोसों के सम्बन्ध में वर्णित आइंस्टाइन के सिद्धान्त के अनुसार किया जाता है। इस सम्बन्ध में प्रयुक्त दोलन आवृत्तियों की गणना रमण प्रभाव और अवरक्त (इनफ्रा-रेड) आवृत्तियों के अध्ययन द्वारा की जाती है। एकपरमाणुक गैसों का नियत ताप पर मोलर ऊष्मा धारिता निम्नलिखित सूत्र से दी जाती है- नीचे की सारणी में कुछ एकपरमाणुक गैसों के वायुमण्दलीय दाब तथा 25 °C ताप पर मोलर स्थिर-आयतन ऊष्मा धारिताएँ दी गयीं हैं। नीचे की सारणी में कुछ द्विपरमाणुक गैसों के मानक ताप (25 °C = 298 K) पर मोलर स्थिर-आयतन ऊष्मा धारिताएँ दी गयीं हैं। द्विपरमाणुक गैसों की नियत-आयतन पर मोलर ऊष्मा धारिताएँ इस सूत्र से प्राप्त की जा सकतीं हैं- किसी वस्तु की विशिष्ट उष्मा ज्ञात करने के लिए सर्वप्रथम उसको ऊँचे ताप तक गरम करते हैं और फिर उसको एक आंशिक रूप से पानी भरे बरतन (कलरीमापी) में डाल देते हैं। वस्तु के ठंडी होने में जितनी कलरियाँ मिलीं उनको कलरीमापी और पानी द्वारा प्राप्त कलरियों के बराबर रखकर विशिष्ट उष्मा की गणना कर लेते हैं। विशिष्ट उष्मा निकालने की एक अन्य विधि यह भी है कि पदार्थ के ऊपर इतनी भाप को प्रवाहित करें कि उसका ताप बढ़कर भाप के ताप के बराबर हो जाए। यदि इस विधि में m ग्राम भाप संघनित (कनडेन्स) होती है तो उसके पानी बनने में m L कलरी प्राप्त होती हैं (L = गुप्त ताप)। इसको पदार्थ द्वारा शोषित उष्मा के बराबर रखकर विशिष्ट उष्मा की गणना कर लेते हैं।
उष्मा, उष्मा-धारिता एवं ताप-परिवर्तन

विशिष्ट उष्मा के सिद्धान्त
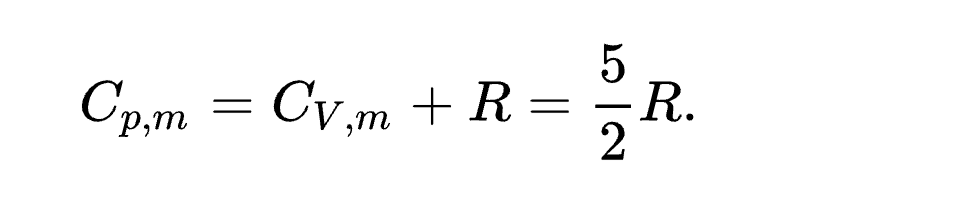
एकपरमाणुक गैस CV, m (J/(mol⋅K)) CV, m/R He 12.5 1.50 Ne 12.5 1.50 Ar 12.5 1.50 Kr 12.5 1.50 Xe 12.5 1.50 द्विपरमाणुक गैस CV, m (J/(mol⋅K)) CV, m/R H2 20.18 2.427 CO 20.2 2.43 N2 19.9 2.39 Cl2 24.1 3.06 Br2 (vapour) 28.2 3.39 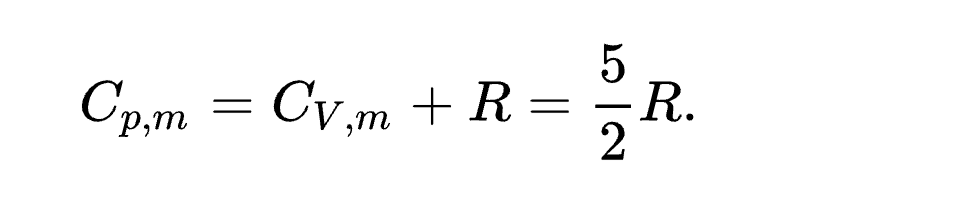
विशिष्ट ऊष्मा का मापन
कुछ पदार्थों की विशिष्ट उष्माएँ
पदार्थ कला या अवस्था
(फेज)Cp
kJ kg−1K−1Cp,m
J mol−1K−1Cv,m
J mol−1K−1आयतनिक
विशिष्ट उष्मा
J cm−3K−1वायुमंडल/वायु (Sea level, dry, 0 °C) गैस 1.0035 29.07 20.7643 0.001297 Air (typical room conditionsA) गैस 1.012 29.19 20.85 एलुमिनियम ठोस 0.897 24.2 2.422 अमोनिया द्रव 4.700 80.08 3.263 Animal (and human) tissue mixed 3.5 - 3.7* एंटीमनी ठोस 0.207 25.2 1.386 आर्गन गैस 0.5203 20.7862 12.4717 आर्सेनिक ठोस 0.328 24.6 1.878 बेरिलियम ठोस 1.82 16.4 3.367 बिस्मथ ठोस 0.123 25.7 1.20 ताँबा (Copper) ठोस 0.385 24.47 3.45 कार्बन डाईआक्साइडCO2 गैस 0.839* 36.94 28.46 हीरा ठोस 0.5091 6.115 1.782 एथनॉल द्रव 2.44 112 1.925 Gasoline द्रव 2.22 228 1.64 काच ठोस 0.84 स्वर्ण ठोस 0.2291 25.42 2.492 ग्रेनाइट ठोस 0.790 2.17 ग्रेफाइट ठोस 0.710 8.53 1.534 हीलियम गैस 5.1932 20.7862 12.4717 हाइड्रोजन गैस 14.30 28.82 हाइड्रोजन सल्फाइड H2S गैस 1.015* 34.60 लोहा ठोस 0.450 25.1 3.537 सीसा ठोस 0.127 26.4 1.44 लिथियम ठोस 3.58 24.8 1.912 मग्नीसियम ठोस 1.02 24.9 1.773 पारा द्रव 0.1395 27.98 1.888 मीथेन 275K गैस 2.191 नाइट्रोजन गैस 1.040 29.12 20.8 निऑन गैस 1.0301 20.7862 12.4717 ऑक्सीजन गैस 0.918 29.38 मोम ठोस 2.5 900 2.325 पॉलीथीन(rotomolding grade) ठोस 2.3027 पॉलीथीन(rotomolding grade) द्रव 2.9308 सिलिका(fused) ठोस 0.703 42.2 1.547 रजत ठोस 0.233 24.9 2.44 टंगस्टन ठोस 0.134 24.8 2.58 यूरेनियम ठोस 0.116 27.7 2.216 [[पानी (वाष्प) gas (100 °C) 2.080 37.47 28.03 पानी द्रव (25 °C) 4.1813 75.327 74.53 4.186 पानी (बर्फ) solid (-10 °C) 2.050 38.09 1.938 जस्ता ठोस 0.387 25.2 2.76 All measurements are at 25 °C unless otherwise noted.
Notable minima and maxima are shown in maroon
Comments Dheeraj on 24-04-2023
नीचे दिए गए विषय पर सवाल जवाब के लिए टॉपिक के लिंक पर क्लिक करें Culture Question Bank International Relations Security and Defence Social Issues English Antonyms English Language English Related Words English Vocabulary Ethics and Values Geography Geography - india Geography -physical Geography-world River Gk GK in Hindi (Samanya Gyan) Hindi language History History - ancient History - medieval History - modern History-world Age Aptitude- Ratio Aptitude-hindi Aptitude-Number System Aptitude-speed and distance Aptitude-Time and works Area Art and Culture Average Decimal Geometry Interest L.C.M.and H.C.F Mixture Number systems Partnership Percentage Pipe and Tanki Profit and loss Ratio Series Simplification Time and distance Train Trigonometry Volume Work and time Biology Chemistry Science Science and Technology Chattishgarh Delhi Gujarat Haryana Jharkhand Jharkhand GK Madhya Pradesh Maharashtra Rajasthan States Uttar Pradesh Uttarakhand Bihar Computer Knowledge Economy Indian culture Physics Polity






Sir formula specific heat